Manning's equation is commonly used to calculate the mean channel velocity of a stream. Manning's equation can be written as
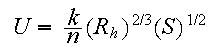
where
Introduction to Hydrology (Geog 3511)
Fall 2012
Assignment 11: Streamflow Analysis
| Section | Lab | Assigned | Due |
| 012,013 | Tuesday | Tuesday, Dec 4 | Friday, Dec 7 |
| 011 | Thursday | Thursday, Dec 6 | Monday, Dec 10 |
40 possible points.
SHOW ALL YOUR WORK.
CITE SOURCES OF EQUATIONS USED.
WRITE THE QUESTION AT THE START OF EACH ANSWER.
Manning's equation is commonly used to calculate the mean
channel
velocity of a stream. Manning's equation can be written as
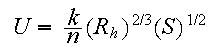
where ![]()
![]() is the
discharge velocity (in m/s),
is the
discharge velocity (in m/s), ![]()
![]() is the
unit conversion factor,
is the
unit conversion factor, ![]()
![]() is the
Manning's n coefficient,
is the
Manning's n coefficient, ![]()
![]() is
the hydraulic radius (in meters), and S is the slope (in meter/meter).
is
the hydraulic radius (in meters), and S is the slope (in meter/meter).
The conversion factor, ![]()
![]() , is
used because the equation is dimensionally inhomogeneous. The value of
, is
used because the equation is dimensionally inhomogeneous. The value of
![]()
![]() depends
on the choice of units used for
depends
on the choice of units used for ![]()
![]() and
and ![]()
![]() .
Because we are using standard metric units (meters for
.
Because we are using standard metric units (meters for ![]()
![]() and meters/sec for
and meters/sec for ![]()
![]() ) the
value of
) the
value of ![]()
![]() is
conveniently 1.0. If you consider the units of
is
conveniently 1.0. If you consider the units of ![]()
![]() , you
would use
, you
would use ![]()
![]() .
.
Manning's ![]()
![]() is a
dimensionless number that characterizes the resistance of the channel
to flow. Higher values of
is a
dimensionless number that characterizes the resistance of the channel
to flow. Higher values of ![]()
![]() indicate greater resistance. Dingman presents a table of typical
Manning's
indicate greater resistance. Dingman presents a table of typical
Manning's ![]()
![]() values (Table 9-6). Also there is a USGS website that lists the n
values of actual rivers.
http://wwwrcamnl.wr.usgs.gov/sws/fieldmethods/Indirects/nvalues/
values (Table 9-6). Also there is a USGS website that lists the n
values of actual rivers.
http://wwwrcamnl.wr.usgs.gov/sws/fieldmethods/Indirects/nvalues/
The hydraulic radius, ![]()
![]() ,
is the cross-sectional area of the stream divided by the wetted
perimeter
,
is the cross-sectional area of the stream divided by the wetted
perimeter
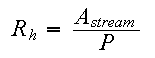
River channels are commonly much wider than they are deep.
Because of this, we sometimes approximate the wetted perimeter of the
channel, ![]()
![]() , by
the width of the channel.
, by
the width of the channel.
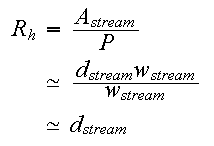
Because area has units of square meters and the perimeter has units of meters, the hydraulic radius also has units of meters.
Bottom roughness of a stream has a large effect on the velocity of water in the channel. Lets solve Mannings equation for mean channel velocity for a smooth sand bed (n=0.025) and a very coarse weedy bed (n=0.075).
Use the following table to answer questions 1 through 4:
| Channel 1 | Channel 2 | |
| cross-sectional area | 12.0 |
12.0 |
| average stream depth | 1.5 |
1.5 |
| channel bottom | smooth sand | weedy bed |
| slope | 0.0006 |
0.0006 |
Q1) What is the hydraulic radius?
Q2) What is mean stream velocity for the channel with a smooth sandy bed?
Q3) What is mean stream velocity for the channel with a weedy bed?
Q4) What is the ratio of ![]()
![]() to
to ![]()
![]() ?
?
Q5) Using the approximation that the channel width is much greater than the depth, rearrange Manning's equation to solve for stream depth. Based on the equation, what effect will an increased slope have on the depth of water? (Note: do not use numbers to answer this question)
Use the following table to answer questions 6 and 7:
| Channel 1 | Channel 2 | |
| mean channel velocity | 2.0 |
2.0 |
| average stream width | 10 |
10 |
| channel bottom | smooth sand | smooth sand |
| slope | 0.0006 |
0.0016 |
Q6) What is mean stream depth for the channel with a lesser slope?
Q7) What is mean stream depth for the channel with a
greater slope?
Q8) Are the answers from questions 6
and 7 realistic in terms of the assumed width/depth ratio?
We can rewrite Manning's equation to calculate the discharge as
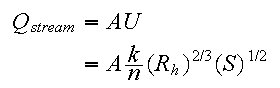
Q9) Using the assumption that the channel width is much greater than the depth, rewrite the preceding equation so that it is in the form
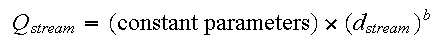
where ![]()
![]() is
the exponent applied to the depth of the stream. (Note: remember that
the hydraulic radius is a function of depth)
is
the exponent applied to the depth of the stream. (Note: remember that
the hydraulic radius is a function of depth)
Q10) Based on the equation derived in Q9, what effect will
an increased depth have on the discharge of the stream? What is the
value of the exponent ![]()
![]() ?
Graph the equation, with the depth of the stream on the x-axis and
discharge on the y-axis.
?
Graph the equation, with the depth of the stream on the x-axis and
discharge on the y-axis.