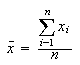
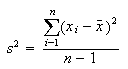
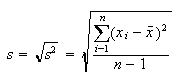
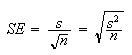
where s is the standard deviation and n is the number of samples
Using a standard statistical package, you should fit a line to the data. This should be done by performing a simple linear regression. The resulting least squares regression line is a best-fit line based on the positions of the data points. The "goodness of fit" of the line is described by the r-squared term such that an r-squared of 1.0 is a perfect fit to the data and an r-squared of 0.0 means there is no relationship between x and y. Another way to think of this is that an r-squared of 0.95 means that x explains 95% of the variability in y.
The least squared regression line can be described by the equation: y = b + mx, the standard equation of a line where b is the y-intercept and m is the slope of the regression line. In many statistical packages, m and b can be found under the heading "coefficients" in the regression output file; b will be the coefficient for the intercept and m will be the coefficient for the x variable.
In order to determine whether the relationship between two variables is significant it is important to look at two values, the r-squared and the "P-value" of the slope of the line. In the case of the r-squared, as values get closer to 1.0, more of the variance in y is explained by x. That is, as the r2 increases (approaches 1.0), more of the y value is explained by the x-values; e.g. more of y is determined by x. However, note that the r2 values DOES NOT tell you whether or not y is significantly related to x.
In the case of the P-value, you want a very low number. A P-value for your slope which is less than 0.05 indicates that you are more than 95% confident in the relationship between the two variables. Similarly, a P-value of less than 0.01 indicates that you are more than 99% confident in the relationship between variables. Often a high r-squared value will lead to a P-value which is much smaller than 0.01 if you have a good number of samples. Remember, the P value that you obtain from the regression analysis in Excel ONLY tells you whether the slope of the line is significantly different than zero. It DOES NOT tell you if y is significantly related to x.