 SNOW HYDROLOGY (GEOG 4321): PHASES OF WATER
SNOW HYDROLOGY (GEOG 4321): PHASES OF WATER  SNOW HYDROLOGY (GEOG 4321): PHASES OF WATER
SNOW HYDROLOGY (GEOG 4321): PHASES OF WATER
Water is one of the few substances that occurs in all three phases on the surface of the earth:
Movement of individual water molecules within a phase and across phases involves energy. Because of the large heat capacity of water, very large amounts of energy are involved in evaporation and freezing. The energy released or used in these activities is one of the major controls on local air temperature, particularly in mountain environments.
The overall relationships among solid, liquid and vapor phases of water are best represented in a single graph known as a phase diagram. A phase diagram shows the conditions at which a substance exists as a solid, liquid or gas as a function of temperature and pressure.
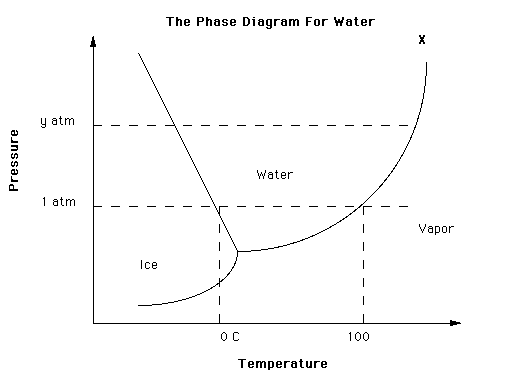
The phase diagram is divided into three regions, each of which represents a pure phase. The line separating any two regions indicates conditions under which these two phases can exist in equilibrium. The point at which all three curves meet is called the triple point. For water, the triple point is at 0.01 deg C and 0.006 atmospheres. This is the only conditions under which all three phases can exist in equilibrium. Note however that call three phases can exist simultaneously at normal pressures and temperatures at the surface of the earth, even though the three phases are not in equilibrium.
Lets change pressure, and see how the boiling point and freezing (melting) point of water deviate from normal magnitueds.
For water at the boiling point, if we increase pressure, we must also increase temperature above 100 deg C for the liquid water to boil. This is how a pressure cooker works. A pressure cooker is simply a sealed container that allows steam to escape only after the steam exceeds a pre-set pressure. As pressure increases above atmospheric pressure, the water in the pressure cooker must exceed 100 deg C before it boils. Looking at the phase diagram, as we increase pressure, we must increase water temperature before the liquid water will boil. Consequently, the liquid water temperature in the pressure cooker can exceed 100 deg C, and the food in the pressure cooker will cook hotter and faster.
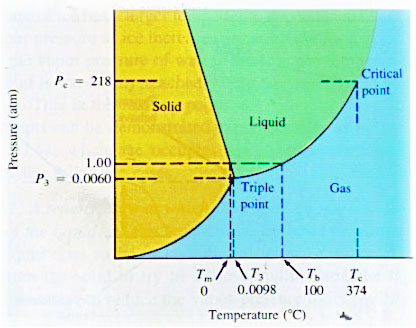
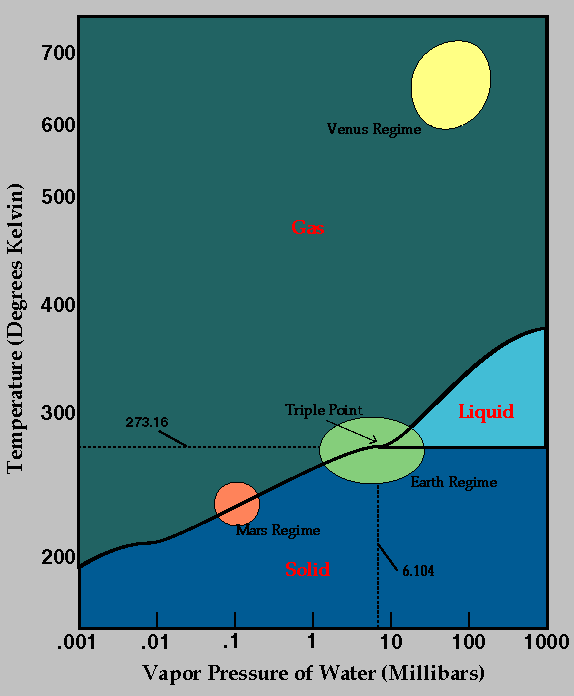
Using phase diagrams,
we can also plot the phases that water
would exist in on other planets:
Energy (q) required for a phase change is equal to the amount of mass (m) of that substance times the latent heat (L) of that phase. For water, we need to know the amount of water in mass units (g or kg) and the phase (ice to liquid or liquid to gas; the reverse directions are the same).
energy required (q) = mass (m) x latent heat (L)
Latent heat (L)
is the amount of heat energy released or absorbed
when a substance changes phase.
The latent heat is a constant for a particular substance
such as water and for a particular phase change
(such as evaporation or freezing).
Units are:
Example
how much energy is required to melt 100 grams of
ice at 0 deg C?
The energy change (q) within a system is a function of the amount of mass (m), the specific heat (c), and the temperature change within the system (delta T):
energy required (q) = mass (m) X specific heat (c) X delta T
Specific energy = amount of heat energy required to raise the temperature of one gram of a substance by one degree C or one degree K.
Example
What is the cold content of a snowpack with an
average temperature of -10 deg c and a mass of 1,000 kg?
The water vapor content of air can be specified in several ways. The "absolute humidity" is expressed as a number density (N v ) of water molecules, or as a mass density (rho v). Meteorologists are inordinately fond of temperatures and pressures, which are directly measurable. Therefore, the amount of water vapor in the air is often expressed as a vapor pressure, given the symbol e.
Ideal gas law is:
PV = N R T, where P pressure N/m^2 V volume m^3 N number of moles R gas constant 8.3143 J/mole-deg T temperature (K) v vapor
Equation of state'' is derived by substituting rho/m for P/V.
P = (rho R T) / m ~~~~~~~~~~ or ~~~~~~~~~~ rho = (P m) / (R T) rho density kg/m^3 m molecular wt kg/mole; air 0.029; water 0.018
Using the Ideal Gas Law and equation of state, we can convert from pressure and volume changes to changes in the mass flux of water.
We can use the Ideal Gas Law to figure out the amount of water vapor in the air, as follows:
Nv = e/kT, or rhov = e/RvTDalton's law states that total pressure is equal to sum of partial pressures. In atmosphere, consider dry air and vapor pressure:
P = Pd + PwDensities may be added also:
rho = rhod + rhow
Saturation vapor pressure
The "maximum" amount of water vapor that is thermodynamically stable is a function of air temperature and has a special name, saturation vapor pressure, or es. "Saturation" is a very poor term, and we are stuck with it. Saturation is a poor term because as we will see, the amount of water vapor in the atmosphere often exceeds the saturation vapor pressure. "Equilibrium vapor pressure" is a more accurate term.
The amount of water vapor that the air can hold increases exponentially with increasing air temperature (T):
es(T) = 0.611 x exp[(17.3T)/(T + 237.3)], where es is in kPa and T is in degree C.
This is an empirical relationship. The 237.3 is not a misprint of 273.2. The true relationship between es(T) and T is a very lengthy formula called the Goff-Gratch equation.Relative humidty (RH) is the ratio of the actual vapor pressure (ea) to the saturation vapor pressure, expressed as a percentage:
RH = ea / es x 100%Supersaturation is when the actual amount of water vapor (or measured vapor pressure) is greater than the saturation vapor pressure. Another way to say this is that supersaturation occurs when the RH is greater than 100%.
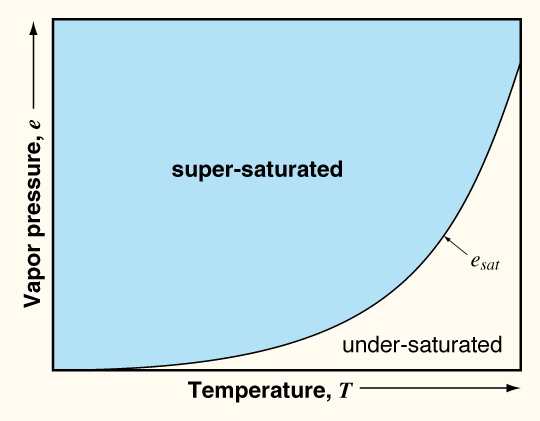
Saturation vapor pressure as a function of temperature.
As we cool an air parcel, we move to the left on the graph above. Consequently, as we cool an air parcel, or the pore space in the snowpack, we can move from a situation where the relative humidity is less than 100% to one where the relative humidity is greater than 100%. In the snowpack, the relative humidity of pore space is always near 100%. Therefore, as water vapor moves from warmer to colder regions in the snowpack, the pore space becomes supersaturated with respect to water vapor and the water vapor deposits (or sublimates) directly from the gas phase to the solid (or ice) phase. The delicate balance between under-and-super-saturated water vapor in the pore space of the seasonal snowpack is what drives such processes as sintering and the formation of depth hoar.
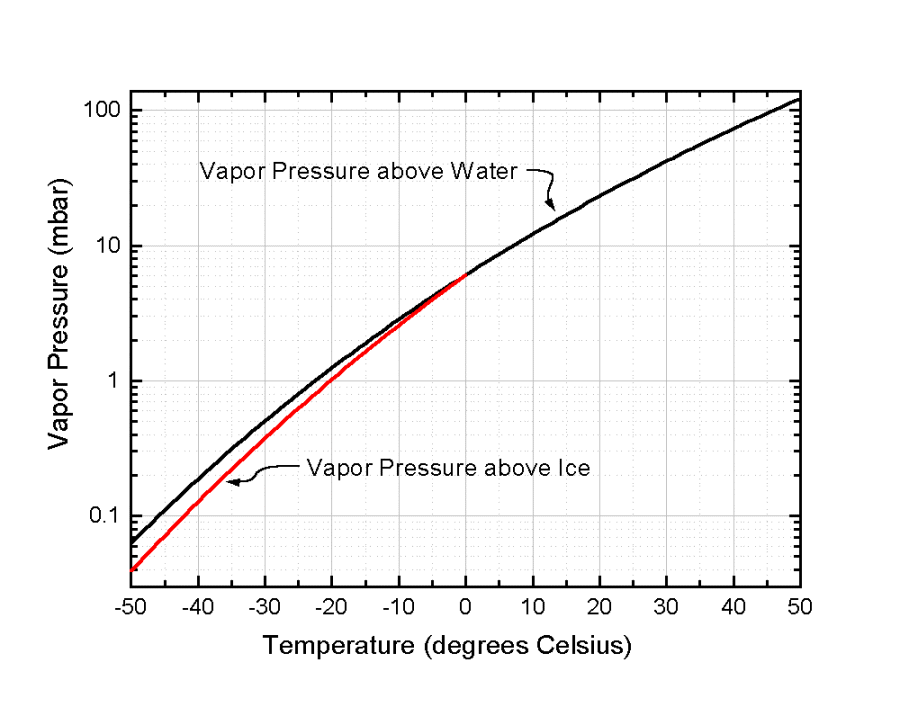
Saturation vapor pressure as a function of temperature for both liquid water and ice.
The following figure provides a clearer demonstration of the difference in saturation vapor pressure between liquid water and ice at the same temperature.
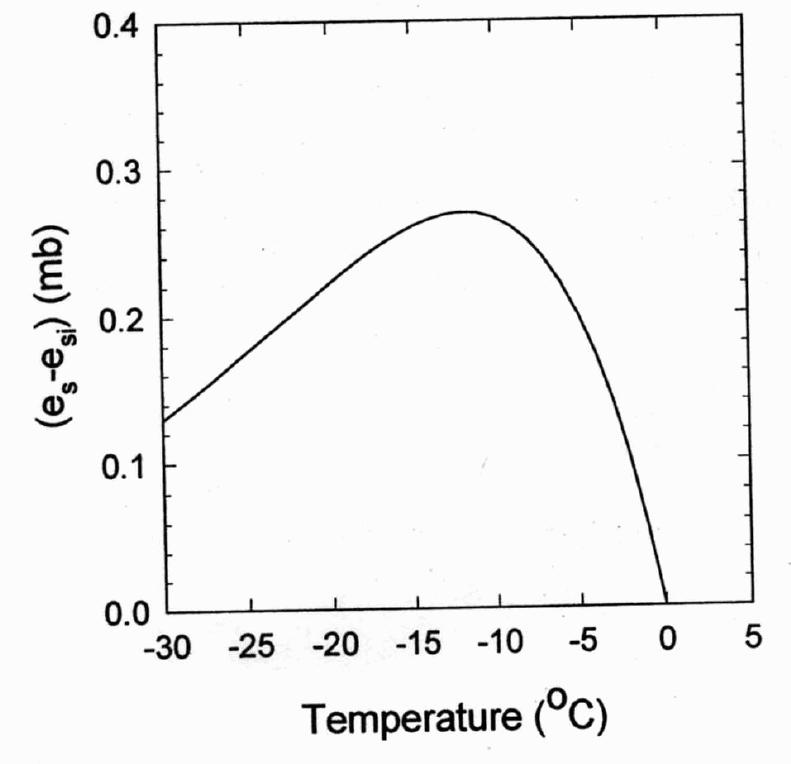
Difference in saturation vapor pressure between liquid water (es) and ice (esi) in mb as a function of temperature. Note that the greatest difference is at -12 degree C.
Because saturation vapor pressure over liquid is always greater than over ice at the same temperature, the atmosphere will be supersaturated with respect to snow crystals when it is not supersaturated with respect to water droplets. Water thus moves by the gas phase from liquid water droplets to ice crystals.
Why is supersaturation important?