Optical Properties of Snow

Optical Properties of Ice

Snow is a matrix of ice grains and air, and, when at 0deg C, it also has a significant fraction of liquid water. Snow also often contains absorbing impurities such as soot, dust, and pollen. The optical properties thus depend on the bulk optical properties and geometry of the ice grains, the liquid water inclusions, and the solid and soluble impurities. In the visible and near-infrared wavelengths, the bulk optical properties of ice and water are very similar, so the reflectance and transmittance of the snowpack in this region of the electromagnetic radiation spectrum depend on the wavelength variation of the refractive index of ice, the grain size distribution of the snow, the depth and density of the snowpack, and the size and amount of those impurities whose refractive indices are substantially different from those of ice and water.

The most important optical property of ice, which causes spectral variation in the reflectance of snow in visible and near-infrared wavelengths, is that the absorption coefficient (i.e. the imaginary part of the refractive index) varies by seven orders of magnitude at wavelengths from 0.4-2.5 micrometers. Normally, the index of refraction is expressed as a complex number, n+ik. The figures below show the real and imaginary parts of the refractive index for ice and water.

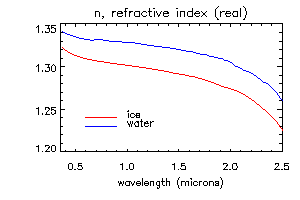
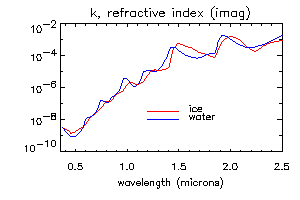
The important properties to note are (1) the spectral variation in the real part n is small and the difference between ice and water may not be significant; (2) the absorption coefficient k of ice and water are very similar, except for the region between 1.35-1.75 micrometers, where ice is slightly more absorptive (subtleties do exist: see Snow Wetness Mapping); (3) in the visible wavelengths, k is very small and ice is transparent; and (4) in the near-infrared wavelengths, ice is moderately absorptive, and the absorption increases with wavelength.

Spectral Characteristics of the Reflectance of Snow

The figure above shows the spectral reflectance of pure deep snow for visible and near-infrared wavelengths, for snow grain radii from 50-1000 micrometers, representing a range for new snow to spring snow, although depth hoar and grain clusters in coarse spring snow can exceed 0.5cm in radius. Because ice is so transparent in the visible wavelengths, increasing the grain size does not appreciably affect the reflectance. The probability that a photon will be absorbed once it enters an ice grain is small, and that probability is not increased very much if the ice grain is larger. In the near-infrared, however, ice is moderately absorptive. Therefore, the reflectance is sensitive to grain size, and the sensitivity is greatest at 1.0-1.3 micrometers (Snow Grain Size Mapping). Because the ice grains are strongly forward-scattering in the near-infrared, reflectance increases with illumination angle, especially for larger grains (figure below).

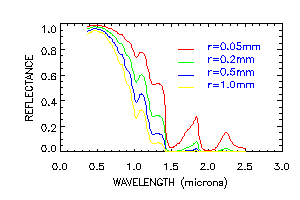
The presence of liquid water in the snow does not by itself greatly affect the reflectance. Except for meltwater ponds in depressions, where melting snow overlies an impermeable substrate, liquid water content in snow rarely exceeds 5 or 6%. This small amount of water does not appreciably affect the bulk radiative-transfer properties, except possibly in those wavelength regions where the absorption coefficients of liquid water and ice are appreciably different. Instead, the changes in reflectance that occur in melting snow in large part result from the increased crystal sizes and from an effective size incrase caused by the two-to-four grain clusters that form in wet unsaturated snow. These apparently behave optically as single grains, causing decreased reflectance in near-infrared wavelengths. It has been observed that the spectral reflectance of a snow sample is lower after warm air is blown over it, but that the reflectance does not increase when the snow is refrozen.

There is no explicit dependence on density for the semiinfinite snowpack, up to densities of ~650kg/m3. The natural increases in density are usually accompanied by increases in grain size; hence, there will be a statistical correlation in field observations carried out over a season, but in an experiment where other variables were held constant, spectrally integrated albedo was measured before and after compacting the snow with a snowmobile and no change was found.

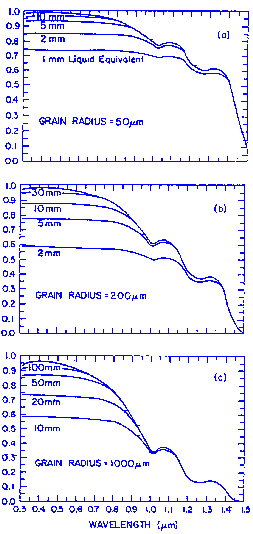
In the visible wavelengths, reflectance is insensitive to grain size, but is affected by two variables, finite depth and the presence of absorbing impurities. The transmission of visible light through snow increases with grain size. The figure below shows the relationship of snow reflectance to snow-water equivalence, for a black substrate, i.e., R = 0. For grain radius r = 1.0mm, the reflectance is perceptibly reduced when the snow amount is reduced to 100mm snow-water equivalence.

Minute amounts of absorbing impurities have been shown to reduce snow reflectance in the visible wavelengths, where ice is highly transparent. The figure below shows that soot concentrations as low as 0.1ppmw (parts per million by weight) are enough to reduce reflectance. The effect of the absorbing impurities is apparently enhanced when they are inside the snow grains because refraction focuses the light on the absorbers.