Unique Properties of Water

Surface Tension is High.

Water beads on a newly-waxed car because the wax is non-polar and does not react with water. Water reacts with itself through hydrogen bonding, forming beads on the car wax. Similarly, water striders "walk" on the surface tension of streams and lakes. Humans could walk on water with special shoes that provided the correct surface area to mass ratio to allow the surface tension of water to support the person.

Viscosity is high.

Viscosity is a measure of how easily a liquid flows. Honey has a high viscosity for example. The hydrogen bonds in water essentially make the water molecule "sticky" for its size, resulting in a high viscosity.

Specific Heat is high.

Specific heat is the amount of energy required to raise the temperature of 1 gram of a substance by 1degC. The specific heat of water is about five times that of land.

• Water can absorb a large amount of heat while its temperature increases only slightly, similarly
• Water will release a lot of heat with only a small drop decrease in temperature.
• The large specific heat of water is why oceans and lakes moderate the climates of adjacent land masses.

Density

Maximum density at 4 degree C, not at freezing point. Expands upon freezing. Lakes only freeze at surface, not bottom.

Melting and boiling points

Abnormally high. Permits water to exist as a liquid at earth's surface.

Solvent properties

Excellent solvent for ionic salts and polar molecules. Important in the transfer of dissolved substances in hydrologic and biological systems.

Molecular Formulas for Water (H₂O)

Electron Distribution in Water Molecule

• Hydrogen
  • single electron
• Oxygen
  • 2 inner electrons in 1s orbital
  • 2 electrons in the 2s orbital
  • 4 electrons in the external 2p orbitals
    • 2_pz = 2; 2_py=1; 2_px = 1
• Water molecule
  • 8 electrons participate in external molecular orbits
    • 2 electrons from hydrogen (one from each hydrogen atom)
    • 6 electrons from 2s and 2p oxygen orbitals
  • Four bonding orbitals results, each with 2 electrons
• 
• The water molecule is therefore dipolar . There is no net charge to the water molecule. However, the electrical field is not evenly distributed on the water molecule. The oxygen atom attracts the electrons more strongly than the hydrogen. This gives water an asymmetrical distribution of charge. The side of the water molecule with the hydrogen atoms has a net positive charge. The side of the water molecule with the two electron orbitals without protons has a net negative charge.
• Molecules that have ends with partial negative and positive charges are known as polar molecules. It is this polar property that allows water to separate polar solute molecules and explains why water can dissolve so many substances.
• A water molecule is formed when two atoms of hydrogen bond covalently with an atom of oxygen. In a covalent bond electrons are shared between atoms. In water the sharing is not equal. The oxygen atom attracts the electrons more strongly than the hydrogen.This gives water an asymmetrical distribution of charge. Molecules that have ends with partial negative and positive charges are known as polar molecules. It is this polar property that allows water to separate polar solute molecules and explains why water can dissolve so many substances.

  

• Hydrogen bonds result from the weak attraction between the negative (or positive) charge on a water molecule with the opposite charge on a neighboring water molecule. The positive regions in one water will attract the negatively charged regions in other waters. The dashes show the hydrogen bond. In a hydrogen bond a hydrogen atom is shared by two other atoms. The donor is the atom to which the hydrogen is more tightly linked. The acceptor (having a partial negative charge) is the atom which attracts the hydrogen atom.

  

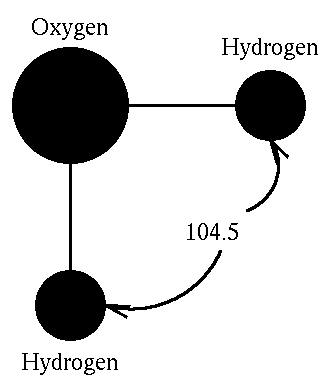
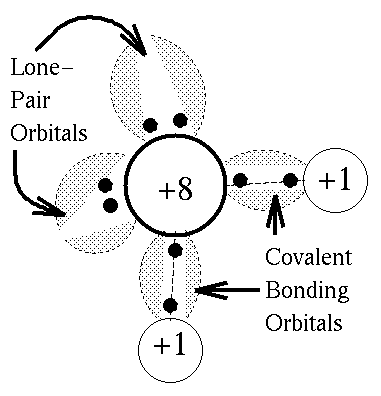
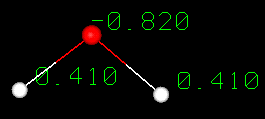
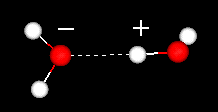
  The hydrogen bond can be regarded as a weak covalent bond, meaning that the energy needed to break it is low - up to 40 KJ/mol, compared with 492 KJ/mol to break one H-O bond in H-O-H. This is the reason why hydrogen bonds ``flicker'' on and off rapidly in liquid water.

• Hydrogen bonds are much weaker than covalent bonds. However, when a large number of hydrogen bonds act in unison they will make a strong contributory effect. This is the case for the liquid state. Liquid water has on average 3.4 hydrogen bonds per water molecule.

  

• Tetrahedral structure
  • The four orbits radiate tetrahedrally from the oxygen nucleus.
  • The two orbits that include the hydrogen atoms do not completely screen the positive charge from the nucleus of the hydrogen atoms.
  • The two orbits without protons (that do not include the hydrogen atoms) provide an excess negative charge in that direction.
  • We can thus picture the ice molecule as a regular tetrahedron with postive charges in two corners and negative charges in two corners. Each possible charge is connected to a different water molecule through hydrogen bonding.
  • 
  • Below is an enlargement that shows the hydrogen bonds connecting two different tetrahedral water crystals.
  • 
• Ice has a rigid lattice structure because in ice each each molecule is hydrogen bonded to 4 other molecules.

  

• Compare the two structures below. Notice the empty spaces within the ice structure.

Ice Ih

• We can define the ice crystalline lattice as the "orderly arrangement of water molecules with fixed positions for the oxygen atoms, held together by hydrogen bonds."
• Okay, to make ice from the water molecule, we need to assemble the water molecules into a three-dimensional lattice. We do so by following these rules:
• BERNAL-FOWLER Ice Rules:
  • There are two protons close to each oxygen atom (about 0.98A)
  • The two protons in each water molecule are oriented so that they point towards two different oxygen atoms
  • There is a single proton on a hydrogen bond between two adjacent oxygen atomos
  • Undee ordinary conditions any of the large number of possible configurations is equally probable.
• MARK'S Ice Rules:
  • Each pair of oxygen atoms is linked by a hydrogen bond.
  • The hydrogen bond moves back and forth between the oxygen atoms.
  • Each oxygen atom in ice is connected to four other oxygen atoms with four hydrogen bonds.
• At normal pressures and temperatures on the surface of the earth, each water molecule in the frozen state forms four hydrogen bonds with O---O distances of 2.76 Angstroms to the nearest oxygen neighbor. The O-O-O angles are 109 degrees, typical of a tetrahedrally coordinated lattice structure.
• 
• Consequently, the basic repeating crystalline structure of the water molecule is a TETRAHEDRON, not a hexagon. A tetrahedron is essentially a 3-dimensional pyramid.
• 
• There are eleven different forms of crystalline ice that are know.
• 
• The hexaganol form known as ice Ih is the only one that is found on the surface of the earth at normal temperatures and pressures.
• A substance in which every atom has four neighbors in a regular tetrahedral structure can crystallize hexagonally or cubically. Ordinary ice has the oxygen atoms of water molecules arranged in layers of hexagonal rings. The atoms in an individual hexagonal ring are not in one plane but in two planes; however alternate atoms are in the upper and lower planes. The spacing between adjacent planes (0.0923 nm) is much less than between layers (hexagonal rings) (0.276 nm). Adjacent layers are mirror images of each other. The structure of the ice crystal is similar to hexagonal metals such as magnesium or cadmium.

• The basal plane is a layer of hexagonal rings. The optic axis or c-axis is at right angles to the basal plane.

  

Solid to Liquid Phase Transition

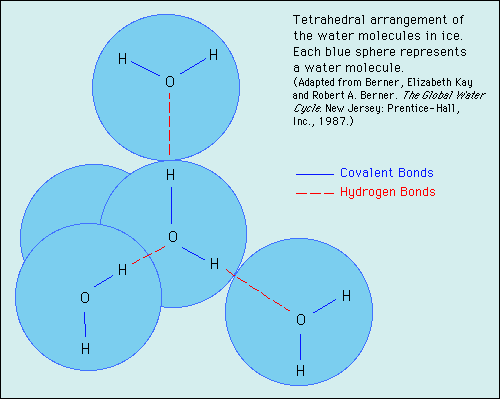
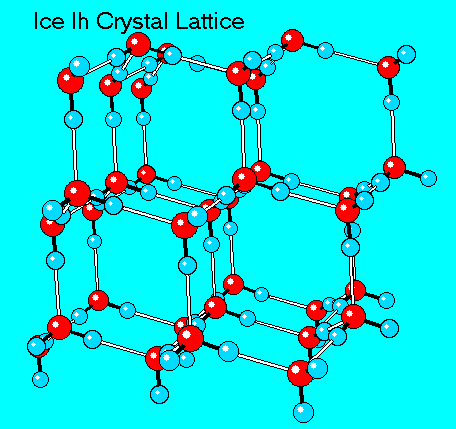
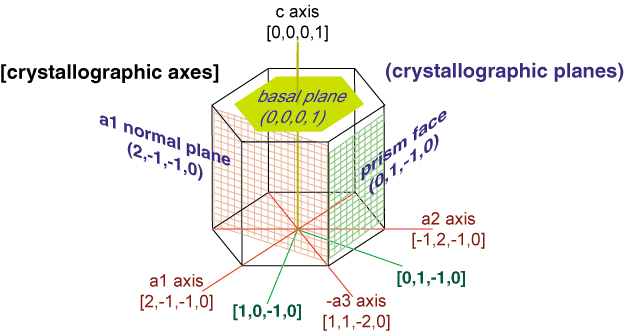
The solid to liquid phase transition is the melting process of ice. Any phase transition occurs due to a change in kinetic energy of the participating particles. If the system is in the solid phase and the kinetic energy is sufficiently increased, the system will go from solid to liquid. In the solid phase, the network strives for the geometrically and bondwise most favoured setup, meaning the lowest energy conformation. In ice, a water molecule has four nearest neighbors to which it is bonded via hydrogen bonds (two from its hydrogen atoms and two from the lone electron pairs on the oxygen). The geometry leads to a rather open hexagonal structure, each of the four bonds representing a lowered overall energy. When the average kinetic energy is raised, the additional jostling begins to destroy the open hexagonal structure. Paradoxically, this allows the molecules to move closer to each other, making and breaking hydrogen bonds much more rapidly. On average, there can now be more than four nearest neighbors at a time, lower energy, and a higher density in the just-melted liquid system. Consequently, in liquid water each molecule is hydrogen bonded to approximately 3.4 other water molecules. In ice each each molecule is hydrogen bonded to 4 other molecules. Therefore the density of ice Ih is 917 kg/m3, compared with a density of 1,000 kg/m3 for liquid water at 4 degC. When rising temperature increases average kinetic energy yet further, molecules move through the liquid so fast that fewer bonds are formed at any one time, shortening the average time each bond exists. The result is higher total energy and thus lower density. So at atmospheric pressure the temperature of greatest density is just above the melting point, at 4 degC Celsius.

QUASI-LIQUID WATER LAYER ON ICE

Coined by Faraday in the 19th century, quasi-liquid is a term describing liquid-like layers that form on solid surfaces at temperatures below the solid's melting point. The quasi-liquid-like layer of the surface of ice at temperatures near the melting point may be a key to many of the processes in snow hydrology. (This section adapted in part from http://electron.lbl.gov/graphs/figures/icetemp.html and http://pearl1.lanl.gov/external/Research/chem_dynamics.htm)

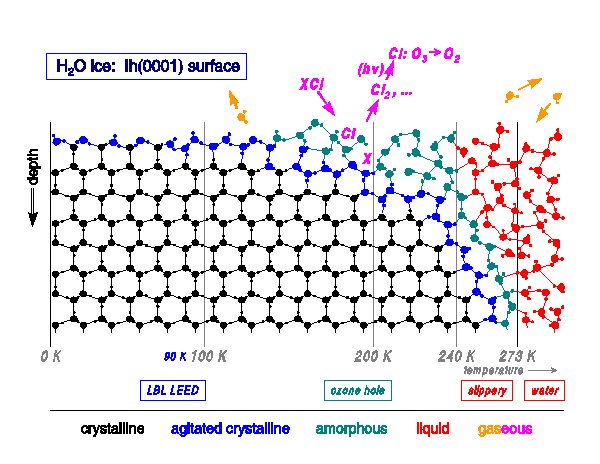
Our proposed evolution of the surface structure of ice is shown with real data from Antarctica as temperature rises from absolute zero (at left) to above the bulk melting point (273 K, at right). Large vibrational amplitudes of the outermost water molecules, still in the crystalline state (blue), exist at extremely cold temperatures. As temperature rises, molecular agitation induces more crystalline defects, yielding an amorphous or quasi-liquid layer (green), as well as evaporation (orange). One important consequence is that, at about 190 K, ice in the Antarctic polar stratospheric clouds catalyzes Cl-containing molecules to Cl2, which in turn is dissociated by sunlight into Cl atoms that decompose ozone (O3): the catalytic action may be due to the amorphous or quasi-liquid ice surface. Above about 240 K (-30 ºC, -20 ºF), the ice surface probably is liquid (red), to a thickness of 10s to 100s of Å:
this permanent liquid film can explain the slipperiness of ice. The quasi-liquid like layer may also explain many of the properties of snow in the atmosphere as well, such as how snowflakes may get larger due to mechanical locking.

For those interested, here's a cool site that chats about two potential unique applications of the quasi-liquid like layer:

• clear power lines of ice, and
• make skiis slipperier by applying an electrical current to the base of the skis.

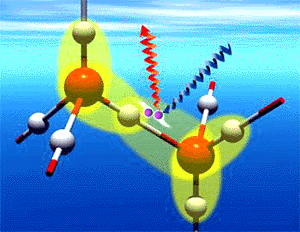
Supplemental information. As mentioned above, the quasi-liquid layers that form on atmospheric ice particles and in the world's snow pack affect the chemistry of those systems and have far-reaching environmental implications. Thus, from being a mere scientific curiosity, the study of these layers has become an inquiry into the mechanisms that drive global change. Preliminary results suggest that both the uptake of organic compounds in snow and the chemistry of tropospheric ozone are affected by the presence of quasi-liquid layers. By studying quasi-liquids in the laboratory with optical techniques, Los Alamos chemists have been able to develop a thermo-dynamic model that predicts the total quasi-liquid volume in the atmosphere and in the snow pack.

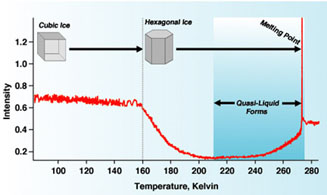
Left: The Los Alamos model suggests that quasi-liquids form in multilayered islands on ice surfaces below the triple point, where solid, liquid, and vapor are in equilibrium.

Right: Ice crystals change from cubic form to hexagonal near 160 K. SHG data supports the Los Alamos model by showing signal for quasi-liquid layers starting at about 212 K and increasing through the melting point.

Additional web sites

Snow Crystals Kenneth Libbrechts' site at CalTech. Probably the single best source on ice physics and snow crystals on the web. Much of the material from this unit from his site.

Water Molecule Home Page from NYU/ACF Scientific Visualization Laboratory

2 Water Molecules Approaching

SUMMARY

• List and describe the importance of at least 6 unique properties of water
• Know the isotopes of water, name, abbreviation, atomic number,
• Be able to draw an single water molecule, label atoms, bonds, charge distribution, etc
• Hydrogen bonds: know and love everything about them.
• Bernal-Fowler rules and Mark's rules: these are the building blocks for crystalline ice
• Crystalline structure: tetrahedron repeating structure, IceIh, density,
• Hexagonal structure: a and c axes, basal plane, optic plane
• Quasi-liquid like nature of ice surface near melting point.

Back to Course Content