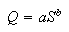
where
Introduction to Hydrology (Geog 3511)
Fall 2012
Assignment 4: Streamflow Analysis
| Section | Lab | Assigned | Due |
| 012,013 | Tuesday | Tuesday, Sep 25 |
Friday, Sep 28 |
| 011 | Thursday | Thursday, Sep 27 |
Monday, Oct 01 |
40 possible points.
SHOW ALL YOUR WORK.
CITE SOURCES OF EQUATIONS USED.
WRITE THE QUESTION AT THE START OF EACH ANSWER.
This lab is based on data that was collected in the Martinelli drainage, at Niwot Ridge. Surface water samples were collected from a seasonal stream draining the 8-ha Martinelli catchment about 400m from the experimental area on Niwot Ridge. The Martinelli catchment has a poorly developed soil structure with little vegetation and is dominated by a late-melting snowpatch [Caine, 1989].
To look at the area on the web, go to:
http://www.topozone.com/map.asp?z=13&n=4433580&e=449163&s=25
The following stage-discharge data were collected in order to define the stage-rating curve.
| Stage(cm) | 12.7 | 10.0 | 9.3 | 6.8 | 2.0 |
| Discharge(l/s) | 19.0 | 10.2 | 3.7 | 2.55 | 0.37 |
Q1) Develop a rating curve for the recorded data. The
rating curve should be of the form
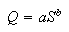
where ![]()
![]() and
and
![]()
![]() are
parameters that are fit using an power regression,
are
parameters that are fit using an power regression, ![]()
![]() is
stage height in centimeters, and
is
stage height in centimeters, and ![]()
![]() is the
discharge in L/s. Plot the data and the rating curve using linear axes
for both the stage and discharge. Report the rating curve equation.
is the
discharge in L/s. Plot the data and the rating curve using linear axes
for both the stage and discharge. Report the rating curve equation.
Q2) Plot the rating curve on log-log coordinates and show the stage - discharge records on the same plot. How well do these data match the curve when plotted in a log-log format?
Q3) Plot the stage height vs. time for July 4 to 18 inc. (use a 10 minute sampling interval)
Q4) Use the rating curve to determine the discharge from July 4 to 18. Plot the discharge vs. time for July 4 to 18 inclusive. (use a 10-minute sampling interval)
Q5) Plot the air temperature for the same time period.
Q6) What date recorded peak flow during this period? Describe the variation in peak flow timing over the two weeks? How is it related to the temperature?
Lets make a seasonal hydrograph using real data from the Martinelli catchment for 1994. You'll need to obtain this data from the Niwot Ridge LTER website:
http://culter.colorado.edu/NWT/
select "Available Data" under Data and agree to the terms.
select Hydrology under "Metadata/data available for core topics" and search for data
select "Streamflow from Martinelli Basin, 1982-"
read the metadata for information on units, etc.
save as text or ascii file (should be the default) or copy and paste the desired date range into EXCEL.
Select the column with the text data and do "Text to Columns" under the Data tab. Choose comma delimited.
Q7) Make a seasonal hydrograph for 1994 using these data. Be sure to label axes and include units. Identify the rising limb and recession limb of the hydrograph.
Q8) On what day or days was peak discharge and what was the amount of peak discharge?
Q9) Estimate the recession coefficient as an average for
the falling flows of the record. Use the data from period 7/14-8/6. The
regression equation is of the form
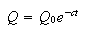
where ![]()
![]() is
the discharge at the start of the regression time period and
is
the discharge at the start of the regression time period and
![]()
![]() is the
exponential regression coefficient. (*Hint: the regression coeffiecient
has units!) Plot the regression curve along with the data for this time
period.
is the
exponential regression coefficient. (*Hint: the regression coeffiecient
has units!) Plot the regression curve along with the data for this time
period.
To accomplish this, there is an example Excel spreadsheet. The example is for 1985 data, so you will need to replace the data (column B) with the appropriate time period. The model calculations (which use the recession curve equations) are in column D. By modifying the parameters Q0 and c (in cells D3 and D4), you can visually fit the model to the data. Cell E5 is the sum of squared error between the data on the model. The lower you can make this value the better your model fit is. The end result you are looking for are the values of Q0 and c that best match the model to the data. Don't forget to adjust the formula in E5 to include the whole dataset! *Hint: To get the best answer, try using the Solver in Excel to minimize the sum of the squared errors.
Q10) Provide a coherent guess as to why peak discharge has such a large and well-defined shape?
Q11) Why is the early summer discharge highly variable, compared to the discharge in late summer?